Sudoku Solving
Published:
Sudoku is an nxn grid based puzzle, typically 9x9, in which the aim is to fill each of the cells with an element from the set (1..n) such that the rows, columns and, in the examples beneath 3x3, sub-grids contain all elements from (1..n). Some of the cells of a puzzle are filled in, these are known as the givens.
There are many different algorithms with varying complexities that can be used to solve a Sudoku but brute force, backtracking, and Dancing Links are discussed, implemented in Ruby, and benchmarked below.
Example Sudoku:
Sudoku Model
The aim, using the strategy pattern, is to produce a family of algorithms that can be interchangeably used to solve a Sudoku. Each algorithm will model a Sudoku puzzle as a single string made from the concatenation of its rows with ‘.’ representing the unknown cells. Thus the example above becomes:
".3..........195....98....6.8...6....4....3..1....2.....6....28....419..5.......7."
and the unique valid solution:
"534678912672195348198342567859761423426853791713924856961537284287419635345286179"
This data structure is encompassed by the Sudoku class. The class provides methods that return arrays of the Sudoku’s rows, columns, and sub-grids respectively. These are calculated from the internal string representation upon method call and the results are cached to reduce the access time of future requests. It also overrides ‘to_s’ for pretty printing and provides getter and setter methods, ‘[]’ and ‘[]=’, for accessing and modifying the internal string, ensuring to invalidate any cached values upon change.
The last method is ‘solve’ that, using dynamic dispatch, will use the given algorithm to return a valid solution (provided one exists).
class Sudoku
def initialize(string)
@string = string
end
def rows
@rows ||= @string.scan(/.{9}/)
end
def columns
@columns ||= rows.map(&:chars).transpose.map(&:join)
end
def sub_grids
return @sub_grids if @sub_grids
grid_builder = Hash.new { |h, k| h[k] = Array.new }
(0...9).each do |i|
(0...9).each do |j|
# 3x3 blocks, numbered 0 to 8, run left to right, top down.
block = (j / 3) + (3 * (i / 3))
grid_builder[block] << rows[i].chars[j]
end
end
@sub_grids = grid_builder.values.map(&:join)
end
def to_s
@string
end
def [](n)
@string[n]
end
def []=(n, v)
@string[n] = v
@rows = @columns = @sub_grids = nil
end
def solve(algorithm)
algorithm.solve(self)
end
end
The first two algorithms, brute force and backtracking, will require a way to check if a possible candidate solution is valid. This can be achieved by implementing methods to test if a candidate meets the three conditions stated above. To keep the code as DRY as possible these will be wrapped in a Solution module and used as a mixin where necessary.
module Solution
private
def solution?(candidate)
valid?(:rows, candidate) &&
valid?(:columns, candidate) &&
valid?(:sub_grids, candidate)
end
def valid?(type, candidate)
candidate.send(type).all? { |a| a.chars.sort == ("1".."9").to_a }
end
end
Brute force
A brute force or exhaustive search algorithm aims to find a solution by enumerating through all possible candidates until one passes. There are 6,670,903,752,021,072,936,960 distinct Sudoku puzzles thus this method is not quick however it does guarantee that a solution will be found provided the puzzle is correct!
The ‘solve’ method iterates through each candidate and returns it if it’s a solution. Checking is made easy by including the Solution mixin shown above. Generating candidates is done in a naive way by enumerating through all possible 81 digit numbers from “111…1” to “999…9”, skipping those that include a 0 or contain values that don’t match the puzzle’s givens.
require_relative 'solution'
require_relative 'sudoku'
class BruteForce
extend Solution
def self.solve(sudoku)
candidates(sudoku).find { |candidate| solution? candidate }
end
private
def self.candidates(sudoku)
return enum_for(:candidates, sudoku) unless block_given?
("1"*81.."9"*81).each do |candidate|
next if candidate.include?("0")
next unless matching_givens?(candidate, sudoku)
yield Sudoku.new(candidate)
end
end
def self.matching_givens?(candidate, sudoku)
# Convert sudoku to regex & match. Works as unknowns are represented by "."
Regexp.new(sudoku.to_s).match(candidate.to_s)
end
end
Backtracking
The backtracking algorithm effectively walks left to right along the string representation of a puzzle replacing unknown cells with a value, ensuring to preserve the invariant that each number in the set (1..9) must be unique in each row, column and sub-grid, and returning the solution if found.
The algorithm backtracks if an unknown value cannot be filled or the end of the string is reached without a solution being found. It does so by walking back to the last unknown cell and replacing it with an unused but still correct value. If there are no possible values then the cell is reset to “.” and the backtracking process repeats.
A logged output of the algorithm solving a Sudoku can be found here.
This can also be thought of as a depth-first traversal of a tree of candidate solutions with the tree’s branches and nodes only being created when required thus reducing the typical space and computation requirements.
The walk, or tree traversal, is handled by the recursive method ‘search’. As ‘search’ modifies the given sudoku it must not be invoked directly. Instead the ‘solve’ method first duplicates the given sudoku and then calls ‘search’, this protects the user from any unexpected side effects.
require_relative 'solution'
require_relative 'sudoku'
class Backtracking
extend Solution
def self.solve(sudoku)
# New copy to avoid changing original sudoku.
temp = Sudoku.new(sudoku.to_s.dup)
search(0, temp)
end
private
def self.search(n, sudoku)
return nil if n > 80
return sudoku if solution?(sudoku)
# Given cell.
if sudoku[n] != "."
return search(n + 1, sudoku)
end
# Unknown cell.
values(n, sudoku).each do |value|
sudoku[n] = value
solution = search(n + 1, sudoku)
return solution if solution
end
# Every possible value explored, reset cell, report no solution.
sudoku[n] = "."
nil
end
def self.values(n, sudoku)
row, column = n / 9, n % 9
sub_grid = (column / 3) + (3 * (row / 3))
('1'..'9').to_a - sudoku.rows[row].chars \
- sudoku.columns[column].chars \
- sudoku.sub_grids[sub_grid].chars
end
end
Dancing Links
Dancing links, also known as DLX, is the technique suggested by Donald Knuth to efficiently implement his Algorithm X. More
“Algorithm X” is the name Donald Knuth used in his paper “Dancing Links” to refer to “the most obvious trial-and-error approach” for finding all solutions to the exact cover problem.
The exact cover problem is represented in Algorithm X using a matrix A consisting of 0s and 1s. The goal is to select a subset of the rows so that the digit 1 appears in each column exactly once. More
The idea of this algorithm is to reduce the problem of solving a Sudoku to that of exact cover. This is achieved by creating a sparse matrix of 0s and 1s that represents a given puzzle, finding a subset of this matrix’s rows such that each column of the combined subset contains exactly one 1, and then transforming these rows back into a solution.
The matrix has four blocks of columns, each 81 bits in length, that correspond to the following constraints:
- Each row can only contain each number once.
- Each column can only contain each number once.
- Each sub-grid can only contain each number once.
- Each cell can only contain one number.
Each row in the matrix represents a certain configuration thus there are four bits per row, one for each constraint.
A visual of the matrix showing all the candidate possibilities and constraints can be found here.
The ‘constraints’ method is used to generate the rows, skipping over any that are invalid due to the given values of the puzzle. These rows are added to a sparse matrix from my implementation of Knuth’s dancing links here and the first set of rows that it returns is converted back into a Sudoku and returned as the solution.
require 'dlx/sparse_matrix'
require_relative 'sudoku'
class DancingLinks
def self.solve(sudoku)
matrix = Dlx::SparseMatrix.new
constraints(sudoku).each { |constraint| matrix.add(constraint) }
matrix.solve { |solution| return convert(solution) }
nil
end
private
def self.constraints(sudoku)
return enum_for(:constraints, sudoku) unless block_given?
(0...9).each do |row|
(0...9).each do |column|
# Cell constraint.
cell_cons = ("0"*((row * 9) + column)) + "1"
cell_cons << "0" * (81 - cell_cons.length)
# Block number.
sub_grid = (column / 3) + (3 * (row / 3))
(0...9).each do |num_index|
string = cell_cons.dup
string << constraint(row, num_index)
string << constraint(column, num_index)
string << constraint(sub_grid, num_index)
num = (num_index + 1).to_s
# Add if number is given.
if sudoku.rows[row][column] == num
yield string
next
end
# Row skip - row already contains n.
next if sudoku.rows[row].include? num
# Column skip - column already contains n.
next if sudoku.columns[column].include? num
# Block skip - sub_grid already contains n.
next if sudoku.sub_grids[sub_grid].include? num
yield string
end
end
end
end
def self.constraint(type_index, num_index)
"0"*9*type_index + "0"*num_index + "1" + "0" * (80 - 9*type_index - num_index)
end
def self.convert(rows)
string = Array.new(81)
rows.each do |row|
chunks = row.scan(/.{81}/)
cell = chunks[0].index("1")
row = cell / 9
column = cell % 9
n = chunks[1].sub("0"*row*9, "").index("1") + 1
string[cell] = n
end
Sudoku.new(string.join)
end
end
Details on how to implement Algorithm X can be found on the wiki page here and the accompanying dancing links page here.
Usage
Complete files to download:
$ ruby -v
ruby 2.2.2p95 (2015-04-13 revision 50295) [x86_64-linux]
$ irb
>> conf.echo = false # Turn off printing return value.
>> load 'sudoku.rb'; load 'brute_force.rb'; load 'backtracking.rb'; load 'dancing_links.rb'
>> s = Sudoku.new("5346789126721...4819834256.85976142342685379....9248569615372842.7419635345286..9")
>> puts s.solve(BruteForce)
# Many years later...
534678912672195348198342567859761423426853791713924856961537284287419635345286179
>> puts s.solve(Backtracking)
534678912672195348198342567859761423426853791713924856961537284287419635345286179
>> puts s.solve(DancingLinks)
534678912672195348198342567859761423426853791713924856961537284287419635345286179
>> exit
Benchmarks
Ideally the same method would be used to benchmark each algorithm however the brute force algorithm is ridiculously slow so it is discussed separately first.
The brute force algorithm took 1714.2 seconds to cycle through 88888888 possible candidates, ~1e-71% of the total number. At worst it would take 1.7142e+76 seconds, or ~5.43e+68 years, to iterate through all candidates. The best case, that the first candidate is a valid solution, takes effectively 0 time thus, on average, it only takes 8.571e+75 years to find a solution!
The remaining two algorithms were benchmarked by recording the average time taken to solve sets of 20000 puzzles, each with a decreasing number of givens.
The sets can be found here.
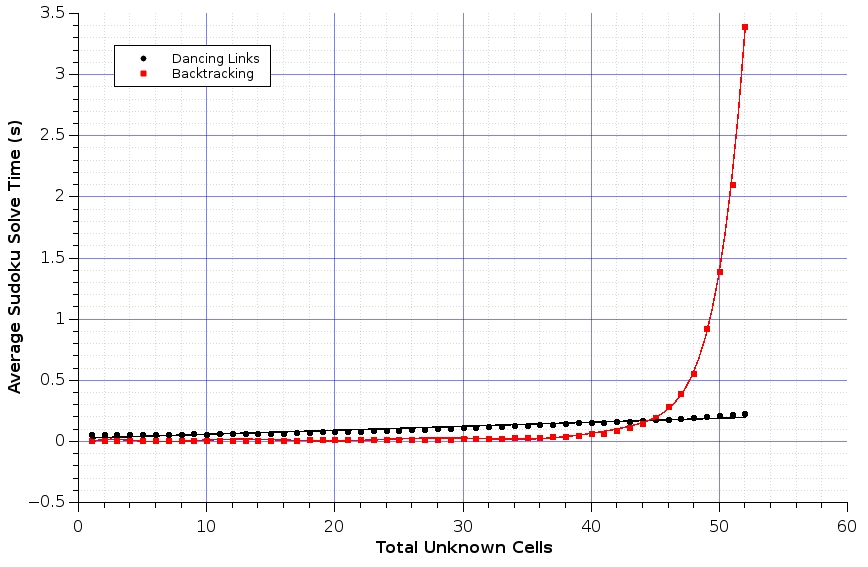
The plot above shows that the dancing links algorithm runs in linear time whilst the backtracking algorithm runs in polynomial time. It should be noted, however, that some of the backtracking algorithm’s large increase in average solve time may be due to cache misses, I’ll update this post after I’ve had time to fully explore this.
Actual numbers can be found here
The above benchmarks were run on my Acer C720 Chromebook running Arch Linux. Processor specs:
$ lscpu
Architecture: x86_64
CPU op-mode(s): 32-bit, 64-bit
Byte Order: Little Endian
CPU(s): 2
On-line CPU(s) list: 0,1
Thread(s) per core: 1
Core(s) per socket: 2
Socket(s): 1
NUMA node(s): 1
Vendor ID: GenuineIntel
CPU family: 6
Model: 69
Model name: Intel(R) Celeron(R) 2955U @ 1.40GHz
Stepping: 1
CPU MHz: 1400.000
CPU max MHz: 1400.0000
CPU min MHz: 800.0000
BogoMIPS: 2794.84
Virtualization: VT-x
L1d cache: 32K
L1i cache: 32K
L2 cache: 256K
L3 cache: 2048K
NUMA node0 CPU(s): 0,1
